The Light Sphere Paradox Of Einstein’s Special Relativity
Unlike the much more famous paradox of the twins, the light sphere paradox is relatively unknown. It forms the basis of the claim that the velocity of light is the same value c in all inertial frames in relative motion. Its paradoxical aspect has not produced the volume of critical discussion or commanded the attention of critics of relativity that it deserves. The author could find only one reference to this paradox in an Internet search and only five references to it in his collection of relativity books.
One issue that needs to be addressed first is that there are different meanings to the concept of paradox. The meaning used by the physics establishment is this definition of paradox: (1) a statement or proposition that seems self-contradictory or absurd but in reality expresses a possible truth. The definition of paradox that this author prefers is the following: (2) a self-contradictory and false proposition. When we review the descriptions of the paradox as presented in the cited physics books it is important to remember that they are using paradox definition (1) and not definition (2). Hence they see no need to fully explain the paradox, since it is merely sufficient to explain that there really is no paradox in the sense of definition (2). The objective of this paper is to demonstrate that it is definition (2) that is the correct understanding of the paradox of the spheres. That is, what is involved is a contradiction that demonstrates that the propositions of relativity are false mathematics.
The background for the paradox can be traced to Einstein’s 1905 paper On the Electrodynamics Of Moving Bodies. Where he introduces the conception of the equivalence of two propagating light spheres. “At the time t=t’=0, when the origin of the coordinates is common to the two systems, let a spherical wave be emitted thereform…The wave under consideration is therefore no less a spherical wave …when viewed in the moving system.” Einstein tells us that the equation of a sphere in the stationary system coordinates is transformed into the equation of a sphere in the moving system coordinates. However, he doesn’t give the proof of this claim, as he says it is obtained “after a simple calculation”. The point at issue here is whether or not Einstein actually proved this claim as he presents it. The proof as he gives it in his 1905 and other papers on relativity is incomplete, and as we will discover in the following, mathematically invalid. Hence this paper will prove that the claim that Einstein proved the covariance of electrodynamics based upon his special relativity kinematics of the Lorentz transformation is false.
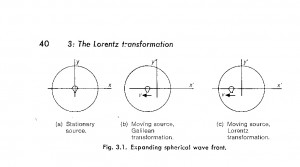
The best introductory discussion of the paradox is presented in Basic Concepts of Relativity, by R. H. Good, pages 39 and 40. Good asks the reader “Suppose a light pulse emitted from a stationary source at the origin at time t=0. It then spreads out with velocity c in a spherical wave front, as seen by an observer at rest relative to the source…Now an observer in another frame of reference moving uniformly in the x direction with velocity v relative to the first frame will also see a spherical wave front spreading out with the velocity c from the origin of his reference frame, assuming that the origins coincide at t=0. This is not what one would expect intuitively; one would expect the sphere of light to remain centered on the source, and consequently to move with different velocities in different directions away from the origin, as seen by the observer in the moving frame.”
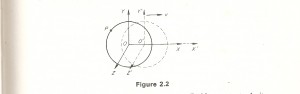
A more puzzling description is given by H. Muirhead in The Special Theory Of Relativity, page 17. Muirhead says “Let us examine what the observers record in the frames Σ and Σ’ in more detail. The observer stationed in Σ (in which the the light source at O is at rest) sees the wave front of the light source from O spreading as a sphere and at any moment in time t, the positions in the wave front are located by the relation x2+y2+z2 =(ct)2 or x2+y2+z2-(ct)2=0. The observer located in Σ’ would also see the light spreading from O’ as a sphere….These two relations can only be satisfied if the two observers see different spheres. We illustrate this point schematically in figure 2.2, where the light spreads from sources O and O’.” This statement is followed by a drawing in which two apparently different coordinate systems Σ and Σ’, with identically the same measurement scales are shown displaced relative to each other, with two different circles drawn with respect to the two different origins. Thus two different displaced or translated circles are shown. The reader is left to contemplate this mystery as the author proceeds to derive the Lorentz transformations based on this illogical mystery, which his version of the theory has presented, but never resolves. Hence the paradox is avoided in the authors mind, but the reader is left stupefied.
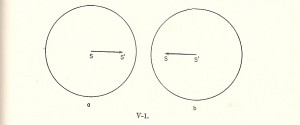
 An elegant solution to the paradoxical difficulties is apparently achieved by Donald H. Menzel in his book Mathematical Physics, pages 376 and 377iv. Menzel prepares the ground by telling the reader that “Einstein pointed the way out of the dilemma.” Menzel describes the problem basically in the same way as does Muirhead, but he adds, “It seems paradoxical even to suggest that the form of the wave front as viewed from S’ could be considered by that observer as a sphere centered at S’. But that is exactly what the relativity postulate requires. The velocity of light, as measured in either system must be a constant. There is no essential difference between S and S’ since both are inertial systems. Thus figure 1b presents the reciprocal conditions from the viewpoint of observer S’.” Figure 1b is drawn as two separated circles, with separated origins S and S’, which are moving in opposite directions. Menzel continues: “Certainly we cannot possibly satisfy (5) and (6), which imply the existence of one sphere with two different centers, if we retain Euclidean ideas of measurement. We have already seen, however, that the the classical concept of simultaneity and therefore of a universal time system runs into difficulties. Perhaps spatial conditions are similarly altered…” He then proceeds to derive the Lorentz transformations without further explanation of their intended meaning.
An elegant solution to the paradoxical difficulties is apparently achieved by Donald H. Menzel in his book Mathematical Physics, pages 376 and 377iv. Menzel prepares the ground by telling the reader that “Einstein pointed the way out of the dilemma.” Menzel describes the problem basically in the same way as does Muirhead, but he adds, “It seems paradoxical even to suggest that the form of the wave front as viewed from S’ could be considered by that observer as a sphere centered at S’. But that is exactly what the relativity postulate requires. The velocity of light, as measured in either system must be a constant. There is no essential difference between S and S’ since both are inertial systems. Thus figure 1b presents the reciprocal conditions from the viewpoint of observer S’.” Figure 1b is drawn as two separated circles, with separated origins S and S’, which are moving in opposite directions. Menzel continues: “Certainly we cannot possibly satisfy (5) and (6), which imply the existence of one sphere with two different centers, if we retain Euclidean ideas of measurement. We have already seen, however, that the the classical concept of simultaneity and therefore of a universal time system runs into difficulties. Perhaps spatial conditions are similarly altered…” He then proceeds to derive the Lorentz transformations without further explanation of their intended meaning.
In his book, Good gives basically the same answer to the paradox as Menzel, “But it follows from Einstein’s second postulate that the light must spread out with velocity v in all directions, in any reference frame, regardless of the motion of the source. Each observer finds that his origin remains at the center of the expanding sphere of light for as long as he continues in uniform motion. And of course each observer finds that the others origin is not at the center. Their disagreement on this point stems from the usual relativistic effects: the Lorentz contraction, time dilation and relativity of simultaneity.”
Standard Resolution Of Paradox
Before we proceed further to discuss the claimed resolutions of the paradox, it is necessary to say something about the two coordinate systems S and S’ and the meaning of coincidence and simultaneity. It is usually not specifically stated what it means when the specification that the two coordinate systems coincide at t=t’=0 is stated as a requirement. Good, Muirhead, Menzel and Schlegel all fail to state clearly what this requirement actually specifies in detail. It is generally assumed by the reader that at the time t=t’=0, that coincidence of the two different coordinate systems S and S’ entails more than just the coincidence or overlapping of the origins, or more precisely the zeros of reference. It is implied that all of the x, y, z and t coordinate numbers are identical with the corresponding x’,y’,z’ and t’ coordinates, because all of these points coincide at t=t’=0. That is the coordinate points are the same, because at t=t’=0 the two different coordinate systems specify the same identical points, because of the coincidence. That is what coincidence means. It is also implied that when the origins coincide, that this is a simultaneous event, and so makes the time scales of both S and S’ simultaneous. That is simultaneous means that the points or events recorded by clocks in S coincide with those in S’.
Einstein in his 1905 paper Reference 1, is more careful about this, but his specification is still a bit sloppy. The reader is, however, led to the notion that what is specified is that the coordinate points of both systems coincide in the meaning given above. There is however, a problem regarding time, in that there is no coincidence of time. That is there is no specification regarding whether the time scales of the systems S and S’ are identical or simultaneous. Here simultaneous has the same meaning for points of the time scale as coincidence does, for the points of the distance scale. Einstein makes the following statement, which seems clear enough, to specify that the times and places of all events are both coincident and simultaneous at the specified coordinate coincidence t=t’=0. He says on page 43: “Let each system be provided with a rigid measuring-rod and a number of clocks, and let the two measuring-rods, and likewise all the clocks of the two systems be in all respects alike.” There is by implication that the clocks are “in all respects alike”, that the events recorded in S have the same time scale or are simultaneous with the same events recorded in S’ for events on the time scale not equal to the simultaneous time of coincidence, t=t’=0. Unfortunately, the reader probably already knows that this is not what Einstein’s theory produces as a result, and so the reader is faced with an obvious contradiction regarding what is specified at the beginning of the purported proof of the special relativity theory.
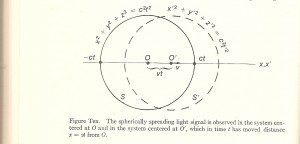
 This section now resumes the discussion of the standard resolution of the paradox of the spheres. In this interpretation, there is no actual paradox to be resolved, because the paradox is an artifact of the correct understanding of the problem. The source for this discussion is taken from a book by Richard Schlegel, Superposition and Interaction, University Of Chicago Press, 1980, pages 82-85. In Figure Ten two different spheres, that is ones which have different centers of expansion, are shown as in the previous three examples of section 2.1. In the figure, the centers of each of the two different spheres are shown as being at the origins O and O’ for the two relatively moving reference frames. Whereas all of the previous authors attributed the resolution of the paradox to relativistic effects in a vague way, Schlegel tells us very specifically how the paradox is resolved: “The application we have made of the Lorentz transformation is to the clocks and rods of systems S and S’. In consequence of their motion relative to each other, they take the specified transformed values. It is important to note that the alterations are purely relational: It is with respect to the x,t (rods and clocks) of one system that the x’,t’ (rods and clocks) of another system have the altered values.” A careful and thoughtful, reader of course, can not accept this if he correctly understood the specification for the two different systems S and S’ given above. That is because the two systems are already in relative motion when the coincidence of the origins takes place at t=t’=0. If it is the relative motion of the coordinate systems that changes the rods and clocks then it is not possible for the specified coincidence to have occurred as specified in the first two paragraphs given above. So what is said as the resolution of the paradox is a contradiction of the stated assumptions.
This section now resumes the discussion of the standard resolution of the paradox of the spheres. In this interpretation, there is no actual paradox to be resolved, because the paradox is an artifact of the correct understanding of the problem. The source for this discussion is taken from a book by Richard Schlegel, Superposition and Interaction, University Of Chicago Press, 1980, pages 82-85. In Figure Ten two different spheres, that is ones which have different centers of expansion, are shown as in the previous three examples of section 2.1. In the figure, the centers of each of the two different spheres are shown as being at the origins O and O’ for the two relatively moving reference frames. Whereas all of the previous authors attributed the resolution of the paradox to relativistic effects in a vague way, Schlegel tells us very specifically how the paradox is resolved: “The application we have made of the Lorentz transformation is to the clocks and rods of systems S and S’. In consequence of their motion relative to each other, they take the specified transformed values. It is important to note that the alterations are purely relational: It is with respect to the x,t (rods and clocks) of one system that the x’,t’ (rods and clocks) of another system have the altered values.” A careful and thoughtful, reader of course, can not accept this if he correctly understood the specification for the two different systems S and S’ given above. That is because the two systems are already in relative motion when the coincidence of the origins takes place at t=t’=0. If it is the relative motion of the coordinate systems that changes the rods and clocks then it is not possible for the specified coincidence to have occurred as specified in the first two paragraphs given above. So what is said as the resolution of the paradox is a contradiction of the stated assumptions.
Schlegel goes on to further explain Figure Ten as follows: “Also, we note that in the spreading-wave illustration as we have presented it there is no postulated physical alteration of the wave front. Rather, it is taken that we have a single, unaltered electromagnetic signal, depicted as a spherically expanding wave. Observers in relatively moving systems S and S’ each find the signal to move with speed c because of the relative changes (Lorentz transformations) which their clocks and rods undergo: the invariance is not a consequence, on this view, of any changes in the electromagnetic wave. But because of the different specifications of simultaneity, the wave front occupies a different set of space points in S, at time t, than it does in S’, at time t’.” The defect with this resolution should be obvious. After telling the reader that the Lorentz transformations change the way the observer measures the single sphere as two different spheres, in the above paragraph, the author compounds the difficulties by giving a different resolution that involves the relativity of simultaneity and changes in time and space. In the first explanation we are supposed to believe that there are two different spheres, because the rods and clocks change, and in the second that there is only one single sphere, because the wavefront occupies two different places and times simultaneously.
To gain a clearer understanding of the difficulty with the standard resolution consider what W. Pauli says in Theory Of Relativity, Dover Publications, 1958, page 9. “At first sight it appears as if the two postulates were incompatible. For, let us take a light source L which moves relative to an observer A with velocity v, and consider a second observer B, at rest with respect to L. Both observers must then see as wave fronts spheres whose centers are at rest relative to A and B respectively. In other words they see different spheres.” This is perplexing since it must be clear that in order to resolve the paradox in the manner proposed, that each observer sees only one sphere and is totally unaware that the sphere looks different to a relatively moving observer. The disagreement only arising when the two of them disagree over where the light source L was located. Was it in S or S’.1
To put it as clearly as possible, in order to resolve the paradox, the two different observers must be persuaded that the spheres are simultaneously the same and different from what they seem to be from observational instruments and rules of procedure. That is the paradox is really to be stated this way. The same sphere is seen to be two different spheres by different observers and the two different observers see two different spheres, that are the same sphere. The spheres are both same and different, simultaneously. So the observers can not agree on the physical reality of what they see. According to the theory of relativity, they must disagree, and this inevitable disagreement can never be resolved. So there is, and always will be, a paradoxical situation that is unresolvable, that is a fundamental law of nature according to the principle of relativity.
Critical Definition Of Paradox -The problem
In this section the definition of the light spheres paradox problem will be described. To understand the difficulty, the problem will be divided into two parts. These two parts reflect the two different aspects of the paradox, although the second aspect is not generally discussed as a paradox. However, before doing that, it is important that we deal with the problem we left in the last section. That is the problem of how a physical phenomena can be both same and different. That is do we have two spheres? Or, only one sphere? Do we have one single physical reality viewed differently, that is the expanding sphere created at the origin of frame S, or do we have two different spheres created at the origins of S and S’? Do we have an expanding light sphere that in frame S seems to have its source in S, or is the source in S’, since the observer there sees it as expanding from his origin O’? Relativity gives us the answer that all of these are the same physical reality, but the facts of observation can only tell us that there is no physical reality that can be determined from experiment, since all of the observational facts lead to contradictions. If the reader doesn’t agree that this is an unsatisfactory situation for a science of nature, then he probably should read no further. That is because the main point of an empirical science is to establish objective facts of reality, or to be able to establish true facts that have a unique empirical basis of justification.
The usual answer to this paradox as given by relativists, is that “According to the principle of relativity, both observers must see the light wave propagating as a spherical wave centered at their respective origins.” But, “If we hold that the position of a wave front is an event permitting description independently in space and time, then we cannot accept this statement as true.” Well that seems obvious and so there must be some escape hatch from the absurdity that the relativity ideology has produced. But the one that is conjured by the relativists, which is based upon the relativity of simultaneity, doesn’t actually work as claimed, because as we will discover, the mathematics behind the claimed proof was done improperly, mainly because the implications of the Lorentz transformations were not carried through to a logical conclusion. That conclusion as we will discover is that the two reference frames can not be in relative motion and produce a consistent system of mathematical equations. Put differently the only mathematically consistent solution that exists in special relativity is the one where the relative motion of reference frames is zero.
Those physicists who advocate that Einstein’s relativity theory is correct tend to confuse objective reality with an observer’s particular viewpoint. They say that what an observer measures is a “just as observed reality” or “just observed” and that this reality can be different for different observers. This leads into the argument that what an observer sees or measures, depends upon his frame of reference, and so it is possible for different observers to observe time and space differently. This type of argument seems profound until one faces the difficulty that if observer at rest in S sees the clocks in S’ as running slow, then it is obvious that the observer in S’ can not at the same time see the clocks in S as also running slow. This is a logical contradiction, as opposed to a reasonable observation by different observers in different reference frames that results in a paradox. A paradox would be if the observer in S sees the clocks of S’ running slow, but that the observer in S’ sees the clocks in S as fast. The paradox being that what the two observers report as objective reality is different. One sees the moving clock being measured as running slow and the other that the clock being measured is fast. This latter situation is not actually a contradiction, but only is a paradox, because the physical objective reality of the situation is covariantly consistent. It is only when the two observers both see the same thing, that is the measured clock is slow in both frames, that there is the contradiction and not a paradox.
Causality Paradox
The main issue regarding the light spheres paradox is as follows. That is if a single event, resulting in a casual physical process, is described as occurring in one of the frames, called the rest or stationary frame, then it is impossible to understand how a coordinate transformation of the physical problem, called a Lorentz transformation, is sufficient to describe an observationally equivalent, in other words the same, physical situation in a different reference frame, the moving frame, when the rods and clocks are specified above. The moving frame S’ being a coordinate reference frame that is in translational motion relative to the first reference frame S is physically different and so must record events differently from the rest frame when the rods and clocks are as required above. This is the same as saying that two different observers experience two different physical processes resulting from the same cause. Put differently, in special relativity physics, the mathematical descriptions of physical processes are not unique, because the same result is recorded relative to two different coordinate systems.
This is the usual way in which a paradox is understood as a contradiction which proves a proposition is false. The falsification contradiction follows from the fact that if the event is to be described with respect to two different physical reference frames, then how is it possible for the same mathematical description to be used for the two different frames? Put differently, the assertion is that the same physical process is described identically in two different coordinate systems of reference. The question then becomes, how is this possible, if the coordinate systems are supposed to be different in terms of relative motion, that they produce the same mathematical description of the physical process? From this it must be concluded that the mathematical description of physical process is not unique in Einstein’s relativity.
The second problem is a restatement of the first difficulty. It is, if the two mathematical descriptions of the same physical process are identical, the usual relativistic description is invariant, then how is it possible to derive equations of transformation that are different from the identity transformation? Put differently, this second paradox arises as a result of the answer that is given to the first paradox. While the first paradox is usually answered, the question that arises from that answer in the form of the second paradox is never addressed. Perhaps another way to state this problem is to ask, are the two apparently different descriptions really describing different things in the same way or simply the same thing, which is supposed to be different in frames S and S’, but isn’t?
In mathematics there is a solution to this difficulty,which avoids the paradox problem. In mathematics, it is required that mathematical systems be unique, such that any mathematical description associated with a coordinate system is unique. Any mathematical description associated with two different coordinate systems that is demonstrated to be the same is resolved by rejecting the contradiction by asserting that such a situation does not involve two different coordinate systems, but the same coordinate system. In formal mathematics this paradoxical, actually contradictory, situation is formally ruled out through the unique identity element theorem. This theorem is also called the theorem of the uniqueness of the null element, the neutral element, or the unit element (0 or 1). The theorem asserts that the element of the algebraic system, which plays the roles of the identity elements or operations must be unique, and from this it follows that the inverse element or operation is also unique.
There is an answer to this problem of causality and uniqueness in special relativity. The answer is that the paradoxical problem is resolved by the mathematical solution of the problem, which shows that the two reference frames S and S’ can not be in relative motion if the observers are at rest relative to both of them, when both observe the same thing, that being a light sphere expanding from the origins O and O’. In other words both observers see the same thing only because they are not in relative motion because the frames S and S’ are at relative rest. The solution is therefore the one demanded by the unique identity element theorem. There can be one and only one coordinate system that allows two different observers to describe a physical process in the same way using identical systems of coordinate measurement. That is the two observers are using the same coordinate system and not two different coordinate systems as is supposed to be the case. Hence the two coordinate systems S and S’ are not in relative motion, but are at relative rest and the paradox is resolved by removing the contradiction.
To make this obscure situation more precise, it should be remembered that the only difference in coordinate systems S and S’ as specified above was the relative motion, and not a difference in the rods and clocks. So the difference in what the observers measure ought to be a result of the relative motion only. Hence the results measured should be different and not the same as claimed by special relativity. On the other hand, if we require that the coordinate systems S and S’ have changed rods and clocks, then it is possible to say that the recorded measurements are the same because the physical process being measured is the same? But this requires that the coordinate systems be different at t=t’=0 which is contrary to the assumptions. Hence the theory is contradicted. So we conclude that the equations of light motion can only be the same for the coordinate systems S and S’ if they are either at relative rest, or have different scales of measure for the rods and clocks. The assumption is that the scales of measure are the same for S and S’ so the conclusion must be there can be no relative motion of S and S’. The paradox, actually a contradiction, being that this is contrary to the claimed proof of the special relativity theory.
The Principle of Relativity Problem
The fundamental claim that Einstein makes is that the light speed postulate is not incompatible with the relativity postulate. The light sphere paradox is a particularly good illustration of the paradoxical difficulty involved in that claim. The obvious solution to the paradox is the following. That is we consider that the velocity of light has a constant component relative to the moving frame caused by the velocity of this frame with respect to the stationary frame. Thus we could solve the problem in this manner. That is the velocity of light in the moving frame has a constant velocity added to it by the relative motion of the frames. All we have to do is apply a Galilean transformation of velocity. But that solution is in violation of Maxwell’s equations. But paradoxically, it is obvious from the statement of the problem and the drawings given that illustrate it, that this is exactly what is supposed to be happening according to the relativity postulate. Hence, we should state the paradox rigorously as follows: According to Maxwell’s equations there should be one and only one, that is a unique, rest frame in which the velocity of light is a constant. According to this principle, there should be one and only one rest frame wherein the light pulse expands as a sphere. In the moving frame the light velocity must not be constant. This contradicts the light velocity constancy postulate. So if we accept the light constancy postulate of Einstein then the relativity postulate produces a contradiction and vice versa.
In Conclusion
The conclusion is that if we accept the postulate regarding the claim that the velocity of light is the same in the two different relatively moving coordinate systems the result is a contradiction. This claim can only be true if there is no relative motion of the coordinate systems S and S’. Hence it is clear that the special relativity theory is based upon a false postulate that must invariably result is contradictions and paradoxes.







I agree with the very good work of Harry H. Ricker. I did not read the books of Good, Muirhead, Menzel or Schlegel. But they all seem to ignore the consequence that the light speed postulate is not compatible with the relativity postulate. The mathematical facts are simple: If light in a moved system (speed v) extends in each direction with speed c, it is necessary that the middle of the light sphere moves with speed v. If the middle of the light sphere is resting, the light cannot have speed c in all directions of a moved system.
There is no paradox!
Stop searching paradox in the Einstein’s relativities!
Do not waste your time!
There are no paradoxes!
What there are: millions of parallel universes (inherent in these theory). One for each observer and sensor.
🙂
This describes very well this world of Alice.
🙂
🙂
Helio
Wolfgang Pauli’s idea: “These two relations can only be satisfied if the two observers see different spheres.”
Did somebody understand Lorentz’s transformation, really?
Note first that the t’-coordinates are strictly bound to some location given by -coordinates.
The t’-values are invalid outside of the position they are assigned to.
If someone write x²-c²t² equals x’²-c²t’² this means to give nonsense some new color.
Any isolated t’-coordinate (without the accompanied x’-value) is meaningless because we don’t have the point where this value is assigned to be true. (As velocity v is oriented in parallel to the x-axis y=y’ and z=z’ are always true.) The Lorentz transformation LT is said to create -pairs out of -pairs. While t is a universal value, valid for any x-value, there is a fundamental difference: LT is creating -pairs out of x-values and the implicit duration needed to travel the distance from 0 to x with v/c. The t’-coordinate therefore tells us the costs (time needed) to reach x by v with respect to reaching v by c.
Now, as you know the meaning of t’, what does x’²+y²=c²t’² mean ? (y=z=0): Therefore: x’² – c²t’² = ds²=0²
How many different points do you find on the circle x’²=c²t’²?
How many spheres will be there as indicated by x’²=c²t’² ?
Einstein did not understand LT.
https://ggsfit.wordpress.com/2016/03/11/a-data-mapping-error/
Einstein did prove that there is a sphere-like formula for every point to be described. What he refrained was to define some unique radius for all points of the same shape, i.e. to conserve the holistic principle of the shape. Einstein gave every point of the shape its own formula. In order to comprehend the fundamental nonsense of Einstein’s ‘proof’ it is important to realize that every point may be described as part of any shape or any object – without restriction and without any proof.
Einstein mapped every point to its very own shape and one spherical shape ends up in as many different shapes as points exist along the x-axis.
Please feel free to read in detail:
https://www.researchgate.net/publication/297759807_DID_EINSTEIN_COMPILE_PERFECT_NONSENSE
To prove all above by yourself you may use the interactive visu of geogebra at:
https://www.geogebra.org/m/HsCX4BjJ
Relativity of simultaneity
From just above, plane waves of star light are coming horizontally. An observer stands on the ground and in front of him, a passenger car is moving to the right. This picture will show that relativity of simultaneity is false (and time dilation also).
Sorry, I cannot receive E-mail. I do not have PC.
http://www.geocities.co.jp/Technopolis/2561/eng.html
Bremsstrahlung
A website says, “A charged particle is decelerated. And energy of motion is emitted as electro magnetic waves”. But deceleration and acceleration will be relative difference seen from inertial frames. Or, phenomenon bremsstrahlung depends on the absolute rest frame?