Carnot Cycle: A New Thermodynamics Perspective
Below is a post on thermodynamics. It’s from Kent Mayhew. I don’t necessarily agree or disagree with his views, but CNPS welcomes new ideas on thermodynamics, so please comment and let us know your thoughts.
In my previous blog (titled: Problematic thermodynamics: A new beginning? Dated Sept 2 2016) I discussed how traditional thermodynamics was a complication of the simple. The real issue being that we wrongly used entropy to explain lost work, when in fact lost work (W=PdV) is simply the energy required to upwardly displace out atmosphere. This has ramifications throughout thermodynamics and all of the sciences.
As a continuation I present this blog, which will show why the currently accepted theory behind the Carnot cycle is misleading, and present a better simpler understanding for the cycle.
I also write this blog in hopes that you will:
- understand why traditional thermodynamics needs an overhaul
- Hopefully you will spot any errors in my analysis so that I may make corrections, as I am only human.
Two good on-line examples demonstrating the traditionally accepted analysis for the Carnot cycle are:
The above webpage gives the currently accepted/used equations. This is the site whose diagrams I shall basically follow in this discussion, that being the diagram used herein (below).
B) https://en.wikipedia. org/wiki/Carnot_cycle
Heat Engine
One of the simplest types of engine is a heat engine wherein power is obtained by the extraction of thermal energy from a heat reservoir. Consider an engine wherein heat () is required for an isobaric expansion process, e.g. the isobaric expansion of a piston-cylinder apparatus filled with an ideal gas. The issue becomes how can this be done at 100% efficiency? It would need to expand due to a heat source and more importantly any realistic system would have to displace our atmosphere, resulting in lost work! Such a possible engine was conceived in the 19th century as follows.
Carnot Engine/Cycle
In 1824, Sadi Carnot envisioned the classic idealistic theoretical heat engine, which is traditionally used to educate young aspiring scientists, known as Carnot Engine/Cycle. Conceptually, his cycle was envisioned as a methodology for extracting energy/work from a constant temperature heat reservoir to be used in some cooler temperature surrounding, or, system. The cycle illustrated in Fig 1.8.12, is based upon traditional interpretations for the compression/expansion cycle of an ideal gas operating between two constant temperature regions, wherein all steps in the process are deemed reversible.
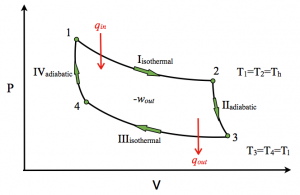
Step 1). “Reversible isothermal expansion”; From points 1 to 2: Put the engine in contact with the hotter heat reservoir at T1, and then allow it to isothermally expand from: V1 to V2. If it were not in contact with the hot reservoir, then the gas’s temperature would have to decrease as it expands, hence does work. The gas’s temperature also increases and this to requires energy. Accordingly, isothermal expansion requires heat in [Q(in)].
Step 2). “Isentropic expansion” as an adiabatic process; From points 2 to 3: The hot engine is thermally re-isolated and its volume is allowed to expand from V2 to V3, until its temperature decreases back to T. Herein the engine cools as it does work in displacing its surroundings i.e. atmosphere.
Step 3). “Reversible isothermal compression”; From points 3 to 4: The engine is now put into thermal contact with a cooler heat reservoir at T ‘ and the gas is now compressed: V3 to V4. In traditional conceptualization the gas gives up energy [Q(out)], i.e. the system’s total energy has decreased.
Step 4). “Isentropic compression” as an adiabatic process; From points 4 to 1: The engine/cycle starts at a colder temperature T ‘and is thermally isolated (100% insulated). The gas is slowly compressed hence its volume decreases from; V4 to V1 and its pressure increases; P4 to P1, which causes to the gas’s temperature increasing to back to T1. And thus completes the cycle.
All the steps of Carnot’s cycle are discussed in terms of theoretically being reversible, hence the cycle is deemed reversible. The cycle’s conceptualizations have been reworked numerous times since and often starts at another steps other than step 1) as described herein.
Contemporary contemplations of the cycle discuss the exchanges of energy (Qin, Qout) with the surroundings but fail to properly describe/define the surroundings, which is a critical error. Rather then adhere to traditional dogma let us now investigate the Carnot cycle employing our new understandings and perspectives.
Our new analysis of the steps
Step 1). “Reversible isothermal expansion”. We realize that the system does work onto its surroundings. Of course if we do clearly not define our surroundings then there is no way to quantify the amount of heat/energy that must enter the system in order for it to remain isothermal. If the surroundings are our atmosphere (as would be for most applications) then insulated expanding systems will cool down, as they upwardly displaces our atmosphere. Logic now dictates that this step is isothermal because the energy in [Q(in)] equates to lost work [W(lost)], then in terms of the atmosphere’s pressure [P(atm)], we can now write:
W(lost) =P(atm)dV eqn (1)
Eqn (1) assumes that our atmosphere is the surroundings, and that this is at 1 atm pressure.
What if the surroundings were a gas filled isometric box. Now there would be no displacement of our atmosphere and the pressure in the surrounding isometric box would increase. Would it increase isothermally, well that depends upon whether or not, the surrounding isometric box was also in thermal contact with the same high temperature isothermal heat source/bath/reservoir (T1=T2=Th). If it was then the work done could be in terms of number of gaseous molecules (N) becomes:
W = -(NkT1)In(V2/V1) = Q(in) eqn (2a)
Or if you prefer in terms of number of mols (n):
W = -(nRT1)In(V2/V1) = Q(in) eqn (2b)
So herein we have just seen that the work required depends upon the system’s surrounding. Accordingly by simply saying surroundings, one cannot expect to know how much work is required. Yet the Carnot cycle as described in contemporary literature i.e. both our on-line examples, seemingly does just that! Interestingly, the on-line example A) uses eqn (2b) to describe the energy requirements, even though nothing is stated about what the surroundings are.
It must be emphasized that in order for any PV engine to be useful to us here on Earth then it must be at some point in its cycle, expand and displace our atmosphere. Any cycle, or step thereof which does not, is only useful when the isometric box acts as the surroundings, hence is limited to motions by devices inside that isometric box. Which is not particularly useful to any of us standing outside the box, here on Earth’s surface.
Now ask is this process reversible. If this is a useful Step in a cycle, therefore it displaces our atmosphere, and then no it is not a reversible step, because lost work is passed onto our atmosphere. Conversely, if it were not a useful step in the cycle then it could be reversible, as could be the case if an isometric box were its surroundings attached to the same hot heat bath. Obviously, there are inherent problems with Step 1) of this Carnot cycle being reversible, if we want to extract any useful from it.
Up to this point we treated the system as being isothermal as the name commonly used for this step implies. But the step is not isothermal, because the system’s/engine’s temperature also increased. Specifically the system was put into contact with a higher temperature heat bath/thermal reservoir to initiate this step.
So we must also consider the amount of thermal energy that has increased inside the system/engine. In terms of the molar specific heat (Cv) and temperature change this energy is:
Q(tempincrease) = nCvdT eqn (3)
Hence the total input of energy required for this non-isothermal step is:
Q(in) = nCv(T’-T) + P(atm)(Vf-Vi) eqn (4)
Eqn (4) assumes that the surroundings are the atmosphere.
Step 2). “Isentropic expansion” as an adiabatic process. This step is deemed adiabatic because it is insulated. Herein the gas continues to expand hence cools; therefore the expanding gas must be doing work onto something. Again there is no clear clarification as to what the surroundings are.
Let us assume that the surroundings are our atmosphere. If this step 1) is cooling down because it is expanding, thus it is displacing our atmosphere, hence it is doing work as would be defined by eqn 1).
It sounds fine until you ask; how does this step actually do any mechanical work? If the system expanded in step 1) and its surroundings were the atmosphere, then logic dictates that the expansion in Step 1) ended at 1 atm pressure. Just because the system is at a higher temperature does not give us the right to think that it is capable of doing any more work. In order for a system to do work onto its surroundings that system must be at a higher pressure. The fact that the system/engine is now at a higher temperature and equal pressure would mean that all it can do is radiate heat. If this heat can be extracted, controlled and then utilized to do work, then so be it, but it still has to be transformed into mechanical energy by some device whose efficiency is 100%.
What if the surroundings were the isometric box? Well now the system/engine can expand only if its pressure is higher than that inside the isometric box. First of all this implies that this is not a useful step in a useful process to us here on Earth’s surface. Secondly; would the expansion in Step 1) not have stopped at the pressure inside the isometric box? If yes then we are back; at how does the system even do any mechanical work?
If there was any real logic behind the expansion described in Step 2) then the energy lost could be calculated using the molar specific heat and temperature change. i.e.:
Q(lost) = nCv(T’-T) eqn (5)
Now ask is this process adiabatic. Does not adiabatic means no exchange of energy whatsoever with its surrounding? Since in Step 2) the system/engine supposedly cools because it is supposedly doing work onto its surroundings. So by definition it is not really an adiabatic process!
Step 3) “Reversible isothermal compression”. Since the compression is isothermal at the colder temperature (Tc=T3=T4), then the ability of the gas to do work does not change I.e. d(PV)=0. The compression of the gas does however require work as defined by either:
W = -(NkT3)In(V4/V3) eqn (6a)
Or:
W = -(nRT3)In(V4/V3) eqn (6b)
Eqn 6a and 6b define the work that results in a pressure increase, hence an increase in the potential to do work, where the potential to do work is with respect to the surroundings. Note that herein we assume that the compression results in a pressure increase with an accompanying molecular volume decrease and that the gas obeys the ideal gas law (PV=NkT).
Since temperature increases occur with compression, then in step 3) there must be heat flowing out of the system in order for the system/engine to be isothermal. Therefore in terms of heat out [Q(out)] we would write
W = -(NkT3)In(V4/V3) = Q(out) eqn (7a)
Or:
W = -(nRT3)In(V4/V3) = Q(out) eqn (7b)
Is step 3) reversible? Yes it seems to be a reversible step in this Carnot cycle.
Step 4). “Isentropic compression” as an adiabatic process. Since the compression is not isothermal, then the ability of the gas to do work does change I.e. d(PV) does not equal 0. The compression of the gas does however require work. If the compression was isothermal then we could write either in terms of the colder temperature (Tc=T3=T4):
W = -(NkT4)In(V1/V4) eqn (8a)
Or:
W = -(nRT4)In(V1/V4) eqn (8b)
However, the compression is not isothermal as described by eqn 8 (a or b). Since the temperature of the system/engine also increased and the thermal energy associated with this temperature increase could be expressed in terms of molecular heat capacity (c_v) and number of molecules (N), then:
Q = Nc_v(T4-T1) eqn (9a)
Or if you prefer in terms of the molar heat capacity (Cv).
Q=nCv(T4-T1) eqn (9b)
Is this step 4) reversible? Yes it is one of the reversible steps in this Carnot cycle.
Traditional Demise
Without going into further detail we should now realize why nobody has actually managed to build a useful idealistic Carnot engine, where the cycle is fully reversible. Obviously, even if the engine was perfectly designed, lost work of expanding systems displacing our atmosphere occurred in step 1) & Step 2) hence, means that its cycle cannot be some useful fully reversible process.
Okay some surroundings may allow for various degrees of reversibility, even in steps 1) & 2) but our reality remains that no useful system/engine wherein a useful step involves expansion that actually powers devices, will ever be reversible, here on Earth’s surface.
In part due to the lost work by useful systems employing the Carnot cycle, both the second law of thermodynamics and its correlation to entropy were conceived. Traditional conceptions were based upon a false pretext for Steps 2 & 3) discussed herein. The pretense that isobaric volume increase (PdV) can be contemplated in terms of an isothermal entropy increase (TdS), became universally accepted:
W = TdS = dE + PdV eqn (10)
Eqn (10) is really part of the basis for entropy’s traditional consideration that related randomness to work. And from here developed the second law concept that such entropy increases could not be reversed without an input of energy.
It is interesting that in some traditional analysis of the Carnot cycle that entropy change is only considered in terms of energy in () or out (), herein entropy is used in place of heat capacity (see: https://en.wikipedia.org/wiki/Carnot_cycle).
TdS = Qin eqn (11)
Of course in considering entropy in terms of heat capacities could make one ponder what does this have to do with randomness?
No matter which version of entropy you prefer, we can see why the Carnot cycle is void of true logic, and our new understanding was readily accomplished without even considering entropy.
The traditional demise actually goes further. Once work was equated to entropy change [eqn(10)], then it seemingly became necessary to think in terms that all forms of work should be expressed in terms of isothermal entropy change. This indoctrinated confusion is now so engrained that the science community now thinks that all work involves entropy changes, rather then limiting such entropy change to lost work as defined by:
W(lost) = P(atm)dV eqn (12)
Yet the sad reality is that all this is nothing more then a continuation of circular logic. Think about it, you design a math to explain empirical data for lost work, and then you exclaim that the empirical data proves your mathematical based theory and then you universally apply it.
To further exasperate the situation, Boltzmann designs his brilliant mathematical conceptualizations (basis of statistical thermodynamics), and determines his constant (k) so that it equates to lost work here on Earth [eqn(12)] for gases. The logic now has been reinforced because now statistical thermodynamics seemingly now explains what we witness, hence is claimed to be inarguable proof, when in actuality it very inception means that it was equated to what was empirically known, hence is a continuation of circular logic.
Ultimately the perception of work in terms of isothermal entropy change, and the proof provided by Boltzmann’s eloquent math are all based upon circular logic, yet this remains fundamental to traditional thermodynamics. Even so, there exists no real readily envisioned explanation for lost work in traditional thermodynamics beyond isothermal entropy change. This theoretical blunder has implications endeared by all the realms of science, often complicating the simple.
Hopefully I have not only demonstrated that both the Carnot cycle and thermodynamics have been poorly conceived over the last century and a half. It is time to end the indoctrination and simplify the science once and for all.
Sincerely Kent Mayhew
Commentary:
It should be stated that any of the equations wherein the work is defined in terms of natural logarithmic function of volume change, can equally be written in terms of natural logarithmic functions of pressure. For example eqn 2a can equally be written in terms of pressure change that being:
W = -(NkT1)In(V2/V1) = (NkT)In(P2/P1)
The above is based upon the realization that work as defined in eqn 2a is based upon the assumption that the ideal gas law is valid, hence pressure multiplied by volume is directly proportional to temperature when defining the gas’s energy.
Understanding some unusual terms used herein.
1) Ability to do work: d(PV). This is really based upon my new understanding that work should not be limited to isobaric isothermal processes as eqn (10) does. Specifically we must start thinking in terms of
W = dE + d(PV) eqn 13
For the isobaric case we could write:
W= dE + PdV eqn 14
The ability to do work has nothing to do with whether or not a system will do work. In order for a system to do work, then its pressure must be greater than the pressure of its surroundings. So you may consider the ability to do work in terms of a system being able to do work against a pressure approaching zero.
2) The potential to do work increases as the pressure increases. I consider the potential to be:
W = VdP eqn 15
3) Useful system is a system that can provide useful energy or power man and/or machine here on Earth’s surface.
It must be emphasized that the above are my terminology based upon my thoughts, which are still in their infancy stage. Accordingly, the terminology may change the future after input is obtained from others. Input from others is always appreciated.
KWM





Dear Nick and Kent,
I fail to understand the concept of “lost work” According to traditional thermodynamics “lost work” means “no work” For work to be done, energy must be given off into the “cold sink” i.e. a surroundings of lower temperature. If there is no cold sink, work cannot be accomplished. Example: Our bodies must do work to maintain our far from equilibrium system. If we are in an environment which is so hot that we cannot give off heat, we die, because our bodies cannot do work. If work were reversible, we should be able to develop a perpetual motion machine. We have not been able to do that and the laws of thermodynamics explain why. True laws of nature are not necessarily logical. They are simply laws. They are what they are. It is the way it is.
Dear Lou
Lost work goes by many names. I have also heard used lost energy. When talking latent heat engineers (& others) often call it non-sensible energy.
Now you say that in traditional thermodynamics lost work means no work. Well first of all if what I say has an relevance then traditional thermo needs an overhaul. Ignoring that then there is a profound difference between lost work and no work. Lost work is energy that is use but cannot be recovered. and now we understand why engineers often refer to it as a non-sensible energy lose. It really makes no sense where this energy goes unless of course you accept what I say.
When I say the term I mean work/energy that is lost by an expanding system performing a task and is lost into the surrounding atmosphere due to changes in the atmosphere’s potential energy. Now lost work will also occur due to friction and numerous other reasons.
Of course in order to explain this lost work traditional thermodynamics came up with ideas like you state, plus they made entropy and its accomplice (the second law) into the explanation as to why expanding systems
experience lost work
So we are at the point. We all accept that expanding system cannot be 100% efficient at providing mechanical work to move man &/or machine. So do we keep with tradition and say its an entropy and second law thing. Or do we rethink what is going on and perhaps start thinking in terms of what I am saying. It must be stated that I am far from perfect, and need other resources and inputs. But right now I stand alone and that is the only fact that I know
Our bodies must do work to survive. I could argue that this is a mammal thing i.e. frogs survive the winter motionless
And yes our environment defines how we evolved – I am not a big fan of creation (sorry if it offends anyone)
And yes a perpetual motion machine is based upon reversibility. reality is we have lost work, whether it be the upward displacement our our atmosphere, or friction etc And if work is lost in a process then that process is certainly not reversible.
Yes the laws of physics based upon entropy and the second law have been manipulated to explain so much like non-reversible. Are you saying so what if they are not based upon any inherent logic. Then fine you are then in a happy place. I am saying that there is a much simpler and logical explanation. So I a stand alone in not so much of a happy place.
Future generations may actually benefit from a logical explanation rather than a science based upon boondoogle But that is not for me to decide, that is for the masses to decide
cheers & thanks Lou for some great insights